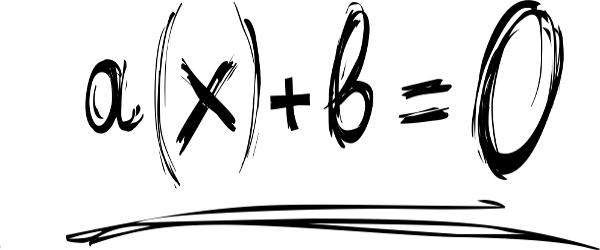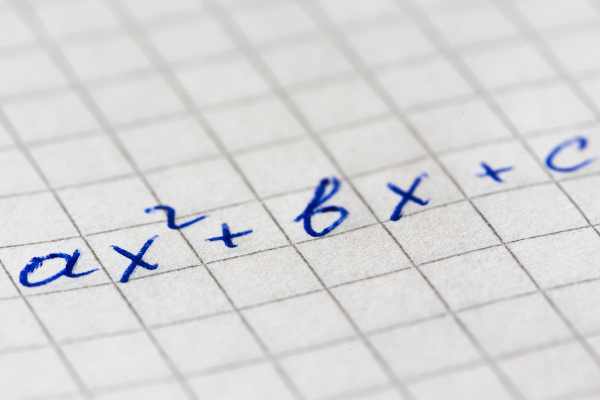Equação exponencial

Equação exponencial é um tipo de equação (sentença matemática que possui incógnitas e uma igualdade) em que a incógnita se encontra no expoente de um ou mais termos. O formato mais simples de uma equação exponencial é . Em muitos casos, é necessário empregar as propriedades de potenciação para resolver uma equação exponencial.

Leia também: Equação produto — a equação que representa a multiplicação de polinômios igualada a zero

Resumo sobre equação exponencial

• Toda equação em que a incógnita aparece no expoente é chamada de equação exponencial.

• Uma das formas de uma equação exponencial é

• Muitas vezes, as propriedades de potenciação são empregadas para resolver uma equação exponencial.

• As principais propriedades da potenciação são:

  • multiplicação de potências de mesma base:

  • divisão de potências de mesma base:

  • potência de potência:

  • potência do produto:

  • potência do quociente:  

• Existem duas formas de resolver equações exponenciais: reduzir à base comum e utilizar a definição de logaritmo.

• Na redução à base comum, para  e , tem-se que

• Na definição do logaritmo, se  e , temos que

Videoaula sobre equação exponencial

O que é a equação exponencial?

Equações são expressões algébricas (expressões matemáticas que contêm números e letras) que apresentam pelo menos um valor desconhecido, chamado de incógnita e representado geralmente por uma letra. Nesse sentido, equação exponencial é a equação em que a incógnita aparece no expoente de um ou mais termos da expressão. Veja os exemplos:

Resolver uma equação significa encontrar o valor da incógnita que torna a igualdade verdadeira, ou seja, que satisfaz a equação. No caso de uma equação exponencial, em que a incógnita está presente no expoente, é fundamental conhecer as propriedades de potenciação para encontrar a solução.

Propriedades da potenciação

Antes de verificar as propriedades da potenciação, fundamentais à resolução de uma equação exponencial, precisamos entender duas notações importantes, as quais veremos a seguir.

• Expoente negativo:

Uma potência com expoente negativo é igual a outra potência cuja base é o inverso multiplicativo da primeira e o expoente é o oposto do primeiro. Formalmente, considerando que x é positivo, temos que

Exemplos:

• Expoente fracionário:

Uma potência de base a com expoente fracionário  é igual a uma raiz com índice n e radicando . Formalmente, temos que

Exemplos:

Partindo disso, vejamos a seguir as principais propriedades da potenciação.

→ Propriedade 1 da potenciação: multiplicação de potências de mesma base

Exemplo:

→ Propriedade 2 da potenciação: divisão de potências de mesma base

Exemplo:

→ Propriedade 3 da potenciação: potência de potência

Exemplo:

Importante: A expressão  não é igual a . Na expressão , o elemento n é expoente da base . Já na expressão , o elemento n é expoente da base m. Considere o exemplo abaixo com ,  e  e note que os resultados são diferentes.

→ Propriedade 4 da potenciação: potência do produto

Exemplo:

→ Propriedade 5 da potenciação: potência do quociente

Exemplo:

Como resolver a equação exponencial?

Para resolver uma equação exponencial de forma algébrica (ou seja, manipulando os termos da expressão), há duas estratégias essenciais: reduzir à base comum e utilizar a definição de logaritmo.

→ Redução à base comum

Nesse tipo de resolução vamos considerar equações exponenciais que podem ser escritas como uma igualdade entre potências de mesma base. Se  e , temos a seguinte relação:

Isso significa que se os dois lados da igualdade possuem a mesma base, então os expoentes são iguais. Esse resultado decorre do estudo das funções exponenciais , que são injetoras.

Exemplo 1:

Qual a raiz da equação ?

Resolução:

Como a base é positiva e diferente de 1, temos que

O conjunto solução é .

Exemplo 2:

Qual a raiz da equação ?

Resolução:

Como a base é positiva e diferente de 1, temos que

O conjunto solução é .

→ Definição de logaritmo

Considere a equação exponencial . Observe que nesse caso não é possível escrever os dois lados da igualdade como potências de mesma base. No entanto, a definição de logaritmo permite explicitar uma solução. Se  e , temos que

Portanto, temos que

Consultando uma tabela de logaritmos ou utilizando a calculadora, obtemos a solução .

Exemplo:

Qual a solução com duas casas decimais da equação ?

Como a base é positiva e diferente de 1, temos que

Consultando uma tabela de logaritmos ou utilizando a calculadora, obtemos a solução .

Veja também: O que é uma função exponencial?

Exercícios resolvidos sobre equação exponencial

Questão 1

(PUC) A soma das soluções reais da equação  é

A)

B)

C) 0

D) 1

E) 2

Resolução

Alternativa C.

Observe que podemos escrever a equação exponencial como uma igualdade de potências de mesma base:

Como a base é positiva e diferente de 1, temos que

Assim, as soluções reais são  e . Logo, .

Questão 2

(PUC) Quanto vale a soma de todas as soluções reais da equação abaixo?

A) 0

B) 1

C) 2

D) 3

E) 4

Resolução:

Alternativa C.

Considere . Assim, podemos reescrever a equação como

Note que  e  são soluções para essa equação do segundo grau. Substituindo  e  na expressão , temos que

Logo, .

Por Maria Luiza Alves Rizzo
Professora de Matemática