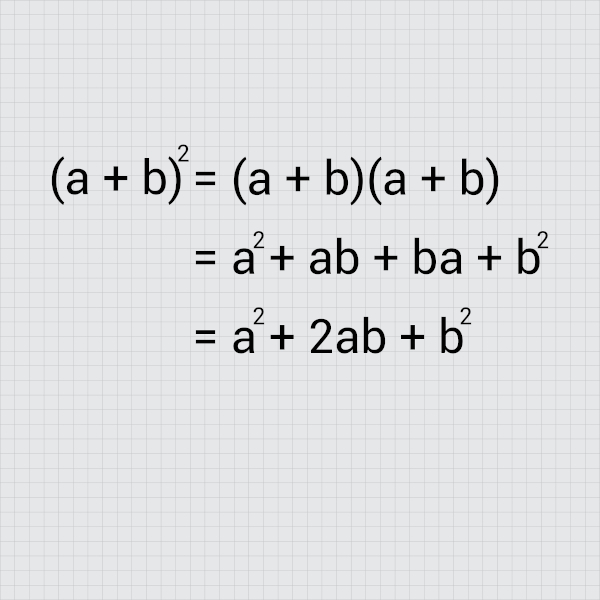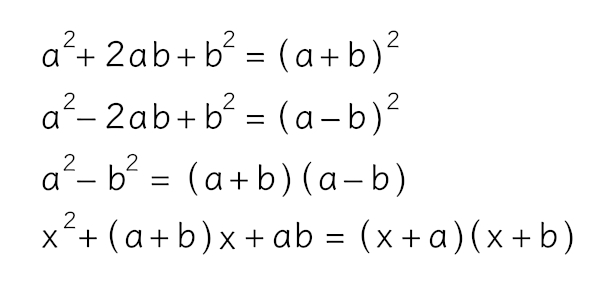
Fatoração e produtos notáveis são dois conceitos muito importantes na álgebra que se conectam diretamente. Ambos ajudam a simplificar expressões algébricas e a resolver equações de forma mais prática.
Leia também: O que é um polinômio?
Resumo sobre fatoração e produtos notáveis
- Fatoração e produtos notáveis são dois conceitos matemáticos que estão conectados.
- Fatorar um polinômio significa representá-lo como a multiplicação de polinômios.
- Os produtos notáveis são usados para fatorar polinômios, especialmente no caso da diferença de dois quadrados, soma de dois cubos e diferença de dois cubos.
- Os casos principais de fatoração são: fator comum em evidência, agrupamento, trinômio quadrado perfeito, diferença de dois quadrados, soma de dois cubos e diferença de dois cubos.
- Os cinco casos principais de produtos notáveis são: quadrado da soma, quadrado da diferença, diferença de dois quadrados, cubo da soma, cubo da diferença e produto da soma pela diferença.
O que é fatoração e produtos notáveis?
Os produtos notáveis são fórmulas que ajudam a simplificar a multiplicação de polinômios, tornando os cálculos mais rápidos e fáceis. Eles envolvem padrões específicos, como o quadrado da soma, o quadrado da diferença, a diferença de dois quadrados, o cubo da soma, o cubo da diferença e o produto da soma pela diferença. Conhecendo os produtos notáveis, podemos expandir ou simplificar expressões algébricas sem precisar fazer as multiplicações passo a passo.
A fatoração de polinômios é basicamente reescrever um polinômio como o produto de dois ou mais polinômios, o que ajuda a simplificar a expressão e facilitar a resolução de problemas.
Relação entre fatoração e produtos notáveis
Para compreender todos os casos de fatoração de polinômio, é fundamental que antes se conheçam os produtos notáveis, pois são eles que nos oferecem os padrões que facilitam o processo de fatoração. Quando estamos realizando a fatoração de um polinômio, estamos reescrevendo-o como um produto entre polinômios e muitas vezes os padrões encontrados ao estudar os produtos notáveis aparecem na expressão algébrica. Reconhecendo esses padrões, podemos fatorar o polinômio, sem precisar fazer o processo completo de multiplicação. Os produtos notáveis são ferramentas essenciais que tornam a fatoração mais simples e ágil.
Veja também: Como simplificar uma fração
Quais são os produtos notáveis?
Conhecemos cinco casos de produtos notáveis:
- quadrado da soma;
- quadrado da diferença;
- diferença de dois quadrados;
- cubo da soma;
- cubo da diferença;
- produto da soma pela diferença.
Vejamos a seguir cada um deles.
→ Quadrado da soma
Quando há a soma entre dois termos elevada ao quadrado:
- Expressão algébrica:
- Caso expandido:
Então, temos que:
→ Quadrado da diferença
Quando há a diferença entre dois termos elevada ao quadrado:
- Expressão algébrica:
- Caso expandido:
De modo geral, temos que:
→ Produto da soma pela diferença
Quando há um produto da soma de dois termos pela diferença entre esses mesmos dois temos:
- Expressão algébrica:
- Caso expandido:
De modo geral, temos que:
→ Cubo da soma
Quando há a soma entre dois termos elevada ao cubo:
- Expressão algébrica:
- Caso expandido:
Logo, temos que:
→ Cubo da diferença
Quando há a soma entre dois termos elevada ao cubo:
- Expressão algébrica:
- Caso expandido:
Então, temos que:
Tipos de fatoração
Os casos de fatoração são:
- fator comum em evidência;
- agrupamento;
- trinômio quadrado perfeito;
- diferença entre dois quadrados;
- soma de dois cubos;
- diferença de dois cubos.
Veremos a seguir cada um deles.
→ Fator comum em evidência
Quando existe um fator comum entre todos os termos do polinômio, podemos utilizar esse método de fatoração, como no exemplo a seguir.
Exemplo:
\(16x^2y + 8xy - 12x^3 \)
Resolução:
Perceba que 12, 8 e 16 são todos múltiplos de 4, logo 4 é fator comum a todos os termos. Agora, analisando as variáveis, note que x aparece pelo menos 1 vez em todos os termos, logo o fator comum é 4x, e o colocaremos em evidência, dividindo cada um dos termos do polinômio por 4x:
\(16x^2y + 8xy - 12x^3 \)
\(4x \left( 4xy + 2y - 3x^2 \right) \)
→ Fatoração por agrupamento
A fatoração por agrupamento é utilizada quando é possível encontrar um fator comum entre os termos de dois a dois.
Exemplo:
Fatore a seguinte expressão:
Resolução:
Separamos os termos em dois grupos:
Agora colocamos o fator comum de cada grupo em evidência:
Percebemos que o termo (x + y) aparece duas vezes, então o colocamos em evidência:
Logo, temos que:
→ Trinômio quadrado perfeito
Durante o estudo dos produtos notáveis, o quadrado da soma ou o quadrado da diferença gera como resultado um trinômio quadrado perfeito, então fatorar um trinômio quadrado perfeito é transformar esse polinômio em um desses produtos.
Temos que:
Exemplo:
Fatore o polinômio a seguir:
Note que:
- x2 é um quadrado perfeito, pois x2 = (x)2.
- 9 também é um quadrado perfeito, pois 9 = 32.
- O termo central é 6x e note que: 6x = 2 ⋅ x ⋅ 3.
Como a expressão segue o padrão de um trinômio quadrado perfeito, ela pode ser reescrita como:
→ Diferença de dois quadrados
A diferença de dois quadrados é outro caso de fatoração derivado de um produto notável.
Sabemos que:
Então reescreveremos um polinômio do tipo a2 - b2 como (a + b) (a - b).
Exemplo:
Fatore o polinômio: x2 – 9.
Resolução:
Sabemos que 9 = 32, então temos a diferença entre dois quadrados perfeitos. Analisando esse polinômio, podemos reescrevê-lo como:
→ Soma de dois cubos
Dada a soma de a3 e b3, podemos fatorar essa soma como:
Exemplo:
Fatore o polinômio 64 + 8x3.
Sabemos que 64 = 43 e que 8a3 = (2a)3, então na forma fatorada, temos que:
→ Diferença de dois cubos
A diferença entre dois cubos pode ser fatorada por:
Exemplo:
Fatore o polinômio: x3 - 8.
Resolução:
Sabemos que 8 = 23, logo temos que:
Saiba mais: Qual a diferença entre monômios e polinômios?
Exercícios resolvidos sobre fatoração e produtos notáveis
Questão 1
Fatore o polinômio:
A)
B)
C)
D)
E)
Resolução: Alternativa B.
Fatorando com o fator comum em evidência, temos que ambos os termos são múltiplos de 3x, logo:
Questão 2
Sabendo que os produtos notáveis são expressões algébricas com padrões definidos, qual é o resultado da expressão a seguir?
A)
B)
C)
D)
E)
Resolução: Alternativa A.
Calculando o produto notável, temos que:
Fontes
BOLDRINI, J. L. et al. Álgebra Linear. 3ª ed. Harbra, 1986.
IEZZI, G.; DOLCE, O.; MACHADO, A. Matemática e Realidade. São Paulo: Atual,2013