Movimento uniformemente variado (MUV)

O movimento uniformemente variado (MUV) é caracterizado por uma aceleração constante e não nula, o que implica que a velocidade do objeto varia em quantidades iguais em intervalos de tempo iguais. As equações que descrevem esse movimento incluem a função horária da velocidade, a função horária do espaço e a equação de Torricelli. O MUV pode ser classificado em dois tipos: com aceleração positiva, quando a velocidade aumenta com relação ao tempo, e com aceleração negativa, quando a velocidade diminui com relação ao tempo.

Leia também: O que é o movimento uniforme (MU)?

Exercícios resolvidos sobre movimento uniforme

Saiba mais

Leis de Newton

Saiba mais

Resumo sobre o movimento uniformemente variado (MUV)

• O movimento uniformemente variado (MUV) é o tipo de movimento que tem uma aceleração constante e não nula, ou seja, a velocidade varia uniformemente ao longo do tempo.
• O MUV é descrito por equações como a função horária da velocidade, a função horária do espaço e a equação de Torricelli.
• Existem dois tipos de MUV: com aceleração positiva, quando a velocidade aumenta ao longo do tempo, e com aceleração negativa, quando há desaceleração.

O que é movimento uniformemente variado (MUV)?

Diferentemente do movimento uniforme (MU), em que a velocidade é constante e, assim, a aceleração é nula, o movimento uniformemente variado (MUV) é o tipo de movimento que tem como característica principal a aceleração escalar não nula e constante, ou seja, uma velocidade escalar que varia uniformemente ao longo do tempo, seja positivamente, seja negativamente. Quando dizemos que a velocidade varia uniformemente ao longo do tempo, queremos dizer que ela varia em quantidades iguais em intervalos de tempo iguais.

Considere o exemplo da seguinte figura:

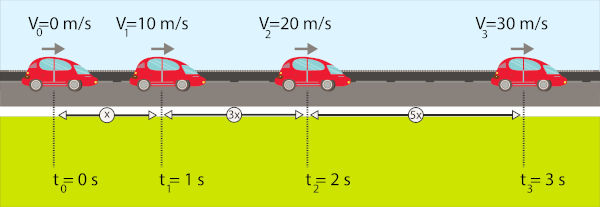
No instante inicial t₀ = 0, o veículo tem uma velocidade inicial de v₀ = 0. Passado um segundo, o veículo passa ter uma velocidade v₁ = 10 m/s. Passado um segundo novamente, o veículo passa ter uma velocidade v₂ = 20 m/s. Por fim, passado mais um segundo, ele passa a ter uma velocidade v₃ = 30 m/s. Dessa forma, a cada segundo, o carro aumenta sua velocidade em mais 10 m/s, portanto, ele tem uma aceleração positiva e constante de a = 10 m/s², caracterizando-se assim um movimento uniformemente variado (MUV).

Fórmulas do movimento uniformemente variado

→ Aceleração escalar (a)

• Δv → variação da velocidade escalar
• Δt → intervalo de tempo

→ Função horária da velocidade escalar para o movimento uniformemente variado (MUV)

\(v = v_0 + a \cdot t \)

• v → velocidade final
• v₀ → velocidade inicial
• a → aceleração
• t → tempo

→ Função horária do espaço escalar para o movimento uniformemente variado (MUV)

\(s = s_0 + v_0 \cdot t + \frac{a \cdot t^2}{2} \)

• s → posição final
• s₀ → posição inicial
• v₀ → velocidade inicial
• a → aceleração
• t → tempo

→ Equação de Torricelli para o movimento uniformemente variado (MUV)

\(v^2 = v_0^2 + 2 \cdot a \cdot \Delta s \)

• v → velocidade final
• v₀ → velocidade inicial
• a → aceleração
• Δs → deslocamento

Como calcular o movimento uniformemente variado (MUV)?

Em um típico problema de movimento uniformemente variado, a fórmula que deve ser utilizada vai depender de quais parâmetros o problema nos ofereceu e qual está exigindo encontrar. A seguir, um exemplo de questão.

• Exemplo:

Um móvel com velocidade inicial de 10 m/s é acelerado uniformemente a 10 m/s². Encontre em quanto tempo o móvel chegará à velocidade de 50 m/s.

Resolução:

Note que o exercício nos forneceu a velocidade inicial, a velocidade final, a aceleração, e quer que encontremos o tempo. Sendo assim, a fórmula que devemos utilizar é a função horária da velocidade escalar para o movimento uniformemente variado:

\(v = v_0 + a \cdot t \\ 50 = 10 + 10 \cdot t \\ 10 \cdot t = 40 \\ t = \frac{40}{10} \\ t = 4 \, \text{s}\)

Tipos de movimento uniformemente variado (MUV)

Existem dois tipos de movimento uniformemente variado, aqueles com aceleração positiva e aqueles com aceleração negativa.

• Aceleração positiva: quando a taxa de variação da velocidade escalar aumenta com relação ao tempo. Por exemplo, quando pisamos no acelerador do carro e sentimos o nosso corpo ir para trás.
• Aceleração negativa: também chamada de desaceleração, ocorre quando a taxa de variação da velocidade escalar diminui com relação ao tempo. Por exemplo, quando pisamos no freio do carro e sentimos o nosso corpo ir para frente.

Acesse também: O que é o movimento circular uniformemente variado (MCUV)?

Exercícios resolvidos sobre movimento uniformemente variado (MUV)

Questão 1

(Faap) Um avião precisa atingir a velocidade de 100 m/s para decolar. Ao partir do repouso, impulsionado por uma aceleração constante, em uma pista de 2000 m, a menor aceleração que deverá ter ao decolar, será de, em m/s²:

A) 5

B) 2,5

C) 1

D) 10

E) 3,5

Resolução:

Alternativa B.

Usando a equação de Torricelli:

\(v^2 = v_0^2 + 2 \cdot a \cdot \Delta s\\ 100^2 = 0 + 2 \cdot a \cdot 2000\\ 10000 = 4000 \cdot a\\ a = \frac{10000}{4000}\\ a = 2,5 \, \text{m/s}^2 \)

Questão 2

(USF) Um ponto material tem movimento regido pela função horária:

\(s = 5 + 2 \cdot t - 2 \cdot t^2 \, (\text{S.I.}) \)

A sua velocidade no instante t=2 s é de:

A) -2 m/s

B) 0

C) 10 m/s

D) 6 m/s

E) -6 m/s

Resolução:

Alternativa E.

Com base na função horária fornecida, temos que v₀ = 2 m/s e a = -4 m/s². Então, usando a função horária da velocidade escalar para o movimento uniformemente variado, para t = 2 s, a velocidade vale:

\(v = v_0 + a \cdot t\\ v = 2 - 4 \cdot 2\\ v = 2 - 8\\ v = -6 \, \text{m/s} \)

Fontes

CARRON, Wilson; GUIMARÃES, Osvaldo. As faces da física (vol. único). 1. ed. Moderna, 1997.

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica (vol. 1). 9 ed. Rio de Janeiro, RJ: LTC, 2012.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.