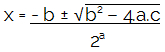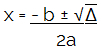O que é Equação do 2° Grau?
Toda equação do tipo ax² + bx + c = 0 é uma equação do 2° grau. Uma das formas de resolvê-la é através da Fórmula de Bhaskara.
Imprimir
Texto:
A+
A-
Escrito por: Amanda Gonçalves Ribeiro
Escritor oficial Brasil Escola
De estudante para estudante
Mande sua pergunta
Artigos Relacionados
O que são equações incompletas do segundo grau?
Clique e aprenda o que são equações incompletas do segundo grau e conheça um método simples de resolvê-las.
O que é Matemática?
O que é concavidade de uma parábola?
Clique e aprenda o que é concavidade de uma parábola e entenda como ela está relacionada aos coeficientes de uma função do segundo grau.
O que é Matemática?
O que é discriminante?
Clique para aprender o que é discriminante de uma equação do segundo grau e descubra como ele pode ser usado para resolver diversos problemas.
O que é Matemática?
O que é equação?
Clique para conferir o que é uma equação, quais são os seus elementos e uma estratégia para resolvê-la!
O que é Matemática?
O que é função do segundo grau?
Clique e descubra o que é uma função do segundo grau e aprenda a encontrar suas raízes e a construir seu gráfico.
O que é Matemática?
O que é fórmula de Bháskara?
Aprenda o que é fórmula de Bháskara e descubra como usá-la para determinar os resultados de uma equação do segundo grau.
O que é Matemática?
O que é o método de completar quadrados?
Clique para aprender o que é o método de completar quadrados, uma das técnicas que podem ser usadas para calcular equações do segundo grau.
O que é Matemática?
Equação do 2º grau sem uso da Fórmula de Báskara
Clique e descubra como resolver uma Equação do 2º grau sem a fórmula de Báskara.
Matemática
O Surgimento da Equação do 2º Grau
Conheça os responsáveis pela resolução de uma equação do 2º grau.
Matemática
Raiz de uma Equação do 2º Grau
Bháskara: Fórmula resolutiva de uma equação do 2º grau.
Matemática
Equação do 2º grau incompleta
Entenda o que é uma equação do 2º grau incompleta, e aprenda como encontrar o conjunto de soluções dela. Resolva os exercícios propostos sobre o tema.
Matemática
Equação do 2º grau
Entenda o que é uma equação do 2º grau. Aprenda como calcular suas raízes e a fórmula de Bhaskara. Saiba também como resolver um sistema de equações do 2º grau.
Matemática
PUBLICIDADE