PUBLICIDADE
Os números complexos surgem a partir da necessidade de resolução de equações que possuem raiz de números negativos, o que, até então, não era possível de resolver-se trabalhando com os números reais. Os números complexos podem ser representados de três formas: a forma algébrica (z = a + bi), composta por uma parte real a e uma parte imaginária b; a forma geométrica, representada no plano complexo conhecido também como plano de Argand-Gauss; e a sua forma trigonométrica, conhecida também como forma polar. Com base na sua representação, como estamos trabalhando com um conjunto numérico, os números complexos possuem operações bem definidas: adição, subtração, multiplicação, divisão e potenciação.
Pela representação geométrica no plano complexo, definimos também o módulo (representado por |z|) de um número complexo — que é a distância do ponto que representa o número complexo até a origem —, e o que é o argumento de um número complexo — que é o ângulo formado entre o eixo horizontal e o seguimento que liga a origem ao ponto que representa o número complexo.
Tópicos deste artigo
- 1 - Necessidade dos números complexos
- 2 - Forma algébrica de um número complexo
- 3 - Operações com números complexos
- 4 - Plano complexo ou plano de Argand-Gauss
- 5 - Forma trigonométrica ou polar
- 6 - Exercícios resolvidos
Necessidade dos números complexos
Na matemática, a ampliação de um conjunto numérico para um novo conjunto, ao longo da história, foi algo bastante comum. Acontece que, nesse decorrer, a matemática desenvolveu-se, e então, para atender as necessidades da época, foi percebido que existiam números que não pertenciam ao conjunto numérico a que se referia. Foi assim com o surgimento dos conjuntos numéricos dos inteiros, dos racionais, dos irracionais e dos reais, e não foi diferente quando houve a necessidade de ampliação do conjunto dos números reais para o dos números complexos.
Ao tentarmos resolver equações do segundo grau, é bastante comum que encontremos a raiz quadrada de um número negativo, o que é impossível de ser resolvido no conjunto dos números reais, por isso a necessidade dos números complexos. O início do estudo desses números recebeu contribuições de matemáticos importantes, como Giralmo Cardono, porém o conjunto deles foi formalizado por Gauss e Argand.
Forma algébrica de um número complexo
Ao tentar-se resolver uma equação do segundo grau, como x² = –25, muitas vezes ela era dita como sem solução. Não obstante, na tentativa de algebrizar, surgiu então a representação algébrica, que possibilita a realização de operações com esses números, ainda que não se consiga calcular a raiz quadrada de um número negativo.
Para facilitar a resolução das situações em que se trabalha com a raiz quadrada de um número negativo, foi definida a unidade imaginária.
![]()
Então, analisando-se a equação apresentada x² = -25, temos que:
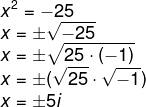
Desse modo, as soluções para a equação são -5i e 5i.
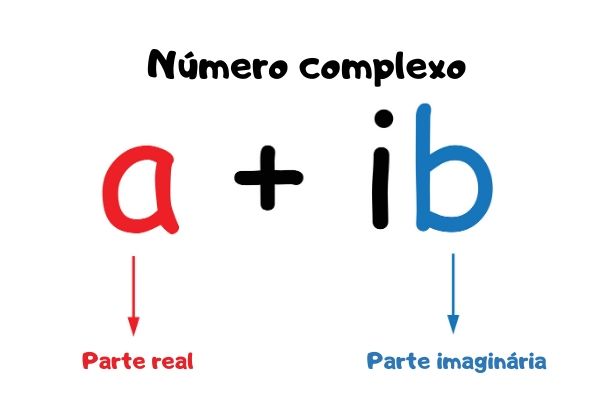
Para definir-se a forma algébrica, foi utilizada a letra i, conhecida como unidade imaginária de um número complexo. Um número complexo é representado por:
z = a + bi
Em que a e b são números reais.
a: parte real, indicada por a = Re(z);
b: parte imaginária, indicada por Im(z);
i: unidade imaginária.
-
Exemplos
a) 2 + 3i
b) -1 + 4i
c) 5 – 0,2i
d) -1 – 3i
Quando a parte real é nula, o número é conhecido como imaginário puro, por exemplo, –5i e 5i são imaginários puros por não possuírem parte real.
Quando a parte imaginária é nula, o número complexo é também um número real.
Operações com números complexos
Como todo conjunto numérico, as operações precisam estar bem definidas, logo, é possível realizar-se as quatro operações básicas dos números complexos levando-se em consideração a forma algébrica apresentada.
-
Adição de dois números complexos
Para realizarmos a adição de dois números complexos z1 e z2, faremos a soma da parte real de z1 e z2 e a soma da parte imaginária, respectivamente.
Seja:
z1 = a + bi
z2 = c + di
z1 + z2 = (a + c) + (b + d)i
-
Exemplo 1
Realização da soma de z1 e z2.
z1 = 2 + 3i
z2 = 1 + 2i
z1 + z2 = (2 + 1) + (3 + 2)i
z1 + z2 = 3 + 5i
-
Exemplo 2
Realização da soma de z1 e z2.
z1 = 5 – 2i
z2 = – 3 + 2i
z1 + z2 = (5 + (–3)) + (–2 + 2)i
z1 + z2 = (5 – 3) + 0i
z1 + z2 = 2 + 0i = 2
Veja também: Representação geométrica da soma de números complexos
-
Subtração de dois números complexos
Antes de falarmos sobre subtração, precisamos definir o que é o inverso de um número complexo, ou seja, z = a + bi. O inverso de z, representado por –z, é o número complexo –z = –a – bi.
Para realizarmos a subtração entre z1 e –z2, assim como na adição, faremos a subtração entre as partes reais e entre as partes imaginárias separadamente, porém é necessário compreender-se que –z2 é o inverso de um número complexo, o que torna necessário a realização do jogo de sinal.
-
Exemplo 1
Realização da subtração de z1 e z2.
z1 = 2 + 3i
z2 = 1 + 2i
z1 – z2 = (2 – 1) + (3 – 2)i
z1 – z2 = 1 + 1i = 1+ i
-
Exemplo 2
Realização da subtração de z1 e z2.
z1 = 5 – 2i
z2 = – 3 + 2i
z1 – z2 = (5 – (–3)) + (–2 – 2)i
z1 – z2 = (5 + 3) + (–4)i
z1 – z2 = 8 + (–4)i
z1 – z2 = 8 –4i
-
Potências da unidade imaginária
Antes de falarmos em multiplicação, precisamos entender a potência da unidade imaginária. Na busca por um método para calcular-se potências de in, é necessário perceber que essas potências comportam-se de forma cíclica. Para isso, vamos calcular algumas potências de i.
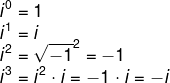
Acontece que as próximas potências nada mais são que a sua repetição, note que:
i 4 = i 2 · i 2 = (–1) (–1) = 1
i 5 = i 2 · i 3 = (–1) (–i) = i
Ao continuarmos a calcular as potências, as respostas sempre serão elementos do conjunto {1,i,–1,–i}, então, para encontrarmos uma potência da unidade i n, faremos a divisão de n (o expoente) por 4, e o resto dessa divisão (r = { 0, 1, 2, 3}) será o novo expoente de i.
-
Exemplo 1
Cálculo de i25
Ao fazermos a divisão de 25 por 4, o quociente será 6 e o resto será igual a 1. Então temos que:
i 25 = i1 = i
-
Exemplo 2
Cálculo de i 403
Ao dividirmos 403 por 4, o quociente será 100, pois 100 · 4 = 400, e o resto será 3, então temos que:
i 403 = i 3 = –i
-
Multiplicação de números complexos
Para realizarmos a multiplicação de dois números complexos, vamos aplicar a propriedade distributiva. Seja:
z1 = a + bi
z2 = c +di, então o produto:
z1 · z2 = (a + bi) (c + di), aplicando a propriedade distributiva,
z1 · z2 = ac + adi + cbi + bdi 2, mas, como vimos, i ² = -1
z1 · z2 = ac + adi + cbi – bd
z1 · z2 = (ac – bd) + (ad + cb)i
Utilizando-nos dessa fórmula, é possível encontrarmos o produto de quaisquer dois números complexos, mas, de modo geral, ela não precisa ser decorada, já que, para o cálculo em questão, basta aplicarmos a propriedade distributiva.
-
Exemplo
Cálculo do produto de (2+3i) (1 – 4i):
(2+3i) (1 – 4i) = 2 – 8i + 3i – 12i ², lembrando que i² = -1:
(2 + 3i) (1 – 4i) = 2 – 8i + 3i + 12
(2 + 3i) (1 – 4i) = (2 + 12) + (– 8 + 3)i
(2+3i) (1 – 4i) = 14 – 5i
Acesse também: Adição, subtração e multiplicação de número complexo
-
Conjugado de um número complexo
Antes de falarmos de divisão, precisamos entender bem o que é o conjugado de um número complexo. O conceito é simples, para encontrarmos o conjugado de um número complexo, basta trocarmos o sinal da parte imaginária.
![]()
-
Divisão de dois números complexos
Para realizarmos a divisão de dois números complexos, precisamos multiplicar a fração pelo conjugado do denominador para que fique bem definido o que é a parte real e o que é a parte imaginária.
![]()
-
Exemplo
Cálculo da divisão de (6 - 4i) : (4 + 2i)
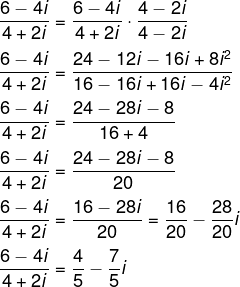
Veja também: Oposto, conjugado e igualdade de números complexos
Plano complexo ou plano de Argand-Gauss
Conhecido como plano complexo ou plano de Argand-Gauss, ele permite a representação na forma geométrica de um número complexo, esse plano é uma adaptação no plano cartesiano para representar números complexos. O eixo horizontal é conhecido como eixo da parte real Re(z), e o eixo vertical é conhecido como eixo da parte imaginária Im(z). Então o número complexo representado por a + bi gera os pontos no plano complexo formado pelo par ordenado (a, b).
-
Exemplo
Representação do número 3 + 2i na forma geométrica Z(3,2).
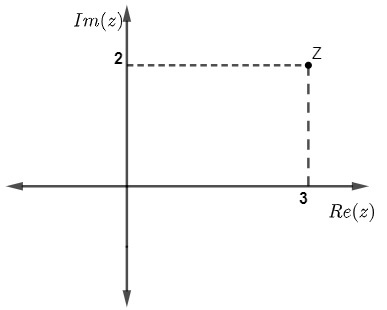
-
Módulo e argumento de um número complexo
O módulo de um número complexo, geometricamente, é a distância do ponto (a,b) que representa esse número no plano complexo até a origem, ou seja, o ponto (0,0).
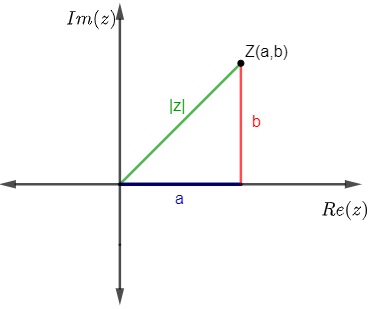
Como podemos perceber, |z| é a hipotenusa do triângulo retângulo, logo, ela pode ser calculada aplicando-se o teorema de Pitágoras, por isso temos que:
![]()
-
Exemplo:
Cálculo do módulo de z = 1 + 3i
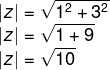
O argumento de um número complexo, geometricamente, é o ângulo formado pelo eixo horizontal e o seguimento |z|.
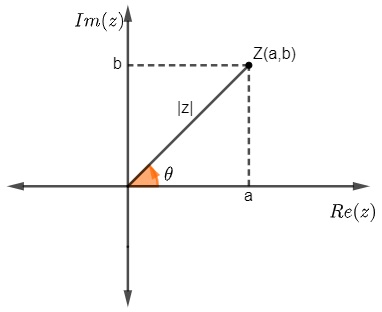
Para encontrar o valor do ângulo, temos que:
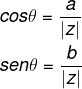
O objetivo é encontrar o ângulo θ = arg z.
-
Exemplo:
Encontre o argumento do número complexo: z = 2 + 2i:
Como a e b são positivos, sabemos que esse ângulo está no primeiro quadrante, então vamos calcular |z|.
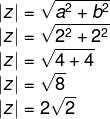
Conhecendo-se o |z|, é possível calcular o seno e o cosseno.
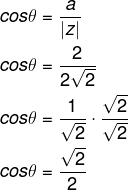
Como, nesse caso, a e b são iguais a 2, então, ao calcularmos o senθ, encontraremos a mesma solução para o cosseno.
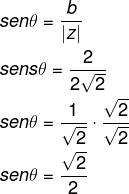
Conhecendo-se os valores de senθ e cosθ, ao consultar-se a tabela dos ângulos notáveis e sabendo-se que θ pertence ao primeiro quadrante, então θ pode ser encontrado em graus ou radianos, logo, conclui-se que:
![]()
Forma trigonométrica ou polar
A representação do número complexo na forma trigonométrica só é possível depois que conseguimos entender o conceito de módulo e argumento. Com base nessa representação, são desenvolvidos conceitos importantes para o estudo dos números complexos a nível mais avançado. Para realizarmos a representação trigonométrica, lembraremo-nos de sua forma algébrica z = a + bi, porém, ao analisarmos o plano complexo, temos que:
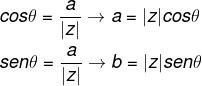
Ao substituirmos, na forma algébrica, os valores de a = |z| cos θ e b = |z| sen θ, temos que:
z = a + bi
Com z = |z| cos θ + |z| sen θ · i, colocando |z| em evidência, chegamos à fórmula da forma trigonométrica:
|
z= |z|(cos θ + i · sen θ) |
-
Exemplo: Escreva, na forma trigonométrica, o número
![]()
Para escrevermos na forma trigonométrica, precisamos do argumento e do módulo de z.
1º passo – Cálculo de |z|
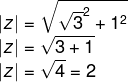
Conhecendo-se o |z|, é possível encontrar-se o valor de θ consultando-se a tabela de ângulos notáveis.
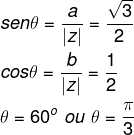
Agora é possível escrever o número z na sua forma trigonométrica com o ângulo em graus ou com o ângulo medido em radianos.
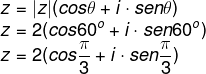
Leia também: Radiciação de números complexos na forma trigonométrica
Exercícios resolvidos
Questão 1 - (UFRGS) Dados os números complexos z1 = (2,–1) e z2 = (3, x), sabe-se que o produto entre z1 e z2 é um número real. Então x é igual a:
a) -6
b) -3/2
c) 0
d) 3/2
e) 6
Resolução
Alternativa D.
Para que o produto seja um número real, então a parte imaginária é igual a zero.
Escrevendo esses números na forma algébrica, temos que:
z1 = 2 – 1i e z2 = 3 + xi
z1 · z2 = (2 – 1i) (3 + xi)
z1 · z2 = 6 + 2xi –3i – xi ²
z1 · z2 = 6 + 2xi –3i + x
z1 · z2 = 6+ x + (2x – 3)i
Como nosso interesse é que a parte imaginária seja igual a zero, então resolveremos 2x – 3 = 0
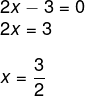
Questão 2 - (UECE) Se i é o número complexo cujo quadrado é igual a -1, então o valor de 5i 227 + i 6 – i 13 é igual a:
a) i + 1
b) 4i –1
c) –6i –1
d) –6i
Resolução
Alternativa C.
Para resolver essa expressão, é necessário encontrar o resto de cada um dos números na divisão por 4.
227 : 4 resulta em quociente 56 e resto 3.
i 227 = i 3 = –i
6 : 4 resulta em quociente 1 e resto 2.
i 6 = i 2 = –1
13 : 4 resulta em quociente 3 e resto 1.
i 13 = i1 = i
Então temos que:
5i 227 + i 6 – i 13
5 (–i) + (–1) – i
–5i –1 – i
–6i – 1
Por Raul Rodrigues de Oliveira
Professor de Matemática






