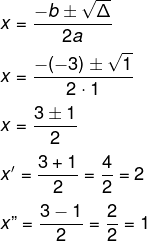PUBLICIDADE
O conceito de matriz inversa se aproxima bastante do conceito de inverso de um número. Vamos lembrar que o inverso de um número n é o número n-1, em que o produto entre os dois é igual ao elemento neutro da multiplicação, ou seja, o número 1. Já a inversa da matriz M é a matriz M-1, em que o produto M · M-1 é igual à matriz identidade In, que nada mais é do que o elemento neutro da multiplicação de matrizes.
Para que a matriz possua inversa, ela precisa ser quadrada e, além disso, o seu determinante tem que ser diferente de zero, caso contrário não haverá inversa. Para encontrar a matriz inversa, utilizamos a equação matricial.
Leia também: Matriz triangular — tipo especial de matriz quadrada
Tópicos deste artigo
- 1 - Matriz identidade
- 2 - Como calcular a matriz inversa
- 3 - Propriedades da matriz inversa
- 4 - Exercícios resolvidos sobre matriz inversa
Matriz identidade
Para compreender o que é a matriz inversa, é necessário antes conhecer a matriz identidade. Conhecemos como matriz identidade a matriz quadrada In em que todos os elementos da diagonal principal são iguais a 1 e os demais termos são iguais a 0.
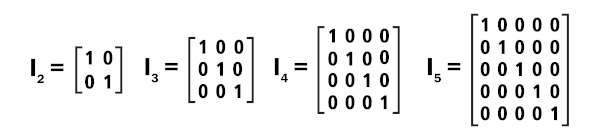
A matriz identidade é o elemento neutro da multiplicação entre matrizes, ou seja, dada uma matriz M de ordem n, o produto entre a matriz M e a matriz In é igual à matriz M.
M · In = M
Como calcular a matriz inversa
Para encontrar a matriz inversa de M, é necessário resolver uma equação matricial:
M · M-1 = In
Exemplo
Encontre a matriz inversa de M.
![]()
Como não conhecemos a matriz inversa, vamos representar essa matriz de forma algébrica:
![]()
Sabemos que o produto entre essas matrizes tem que ser igual a I2:
![]()
Agora vamos resolver a equação matricial:
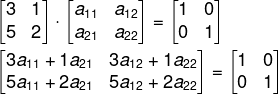
É possível separar o problema em dois sistemas de equações. O primeiro usa a primeira coluna da matriz M ·M-1 e a primeira coluna da matriz identidade. Assim, temos que:
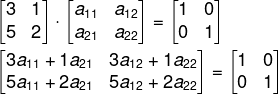
Para resolver o sistema, vamos isolar a21 na equação II e substituir na equação I.
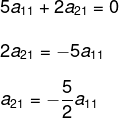
Substituindo na equação I, temos que:
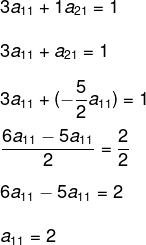
Como encontramos o valor de a11, então encontraremos o valor de a21:
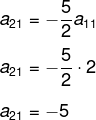
Conhecendo o valor de a21 e a11, agora encontraremos o valor dos demais termos montando o segundo sistema:
![]()
Isolando a22 na equação III, temos que:
3a12 + 1a22 = 0
a22 = – 3a12
Substituindo na equação IV:
5a12 + 2a22 =1
5a12 + 2·( – 3a12) = 1
5a12 – 6a12 = 1
– a12 = 1 ( – 1)
a12 = – 1
Sabendo o valor de a12, encontraremos o valor de a22 :
a22 = – 3a12
a22 = – 3 · ( – 1)
a22 = 3
Agora que conhecemos todos os termos da matriz M-1, é possível representá-la:
![]()
Leia também: Adição e subtração de matrizes
Propriedades da matriz inversa
Existem propriedades que resultam da definição de uma matriz inversa.
- 1ª propriedade: a inversa da matriz M-1 é igual à matriz M. A inversa de uma matriz inversa é sempre a própria matriz, ou seja, (M-1)-1 = M, pois sabemos que M-1 · M = In, portanto M-1 é a inversa de M e também M é a inversa de M-1.
- 2ª propriedade: a inversa de uma matriz identidade é ela mesma: I-1 = I, pois o produto da matriz identidade por ela mesma resulta na matriz identidade, ou seja, In · In = In.
- 3ª propriedade: a inversa do produto de duas matrizes é igual ao produto das inversas:
(M×A)-1 = M-1 · A-1.
- 4ª propriedade: uma matriz quadrada possui inversa se, e somente se, o seu determinante é diferente de 0, ou seja, det(M) ≠ 0.
Exercícios resolvidos sobre matriz inversa
1) Dadas a matriz A e a matriz B, sabendo que elas são inversas, então o valor de x+y é:
![]()
a) 2.
b) 1.
c) 0.
d) -1.
e) -2.
Resolução:
Alternativa d.
Montando a equação:
A · B = I
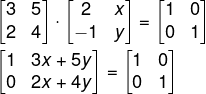
Pela segunda coluna, igualando os termos, temos que:
3x + 5y = 0 → (I)
2x + 4y = 1 → (II)
Isolando x em I:
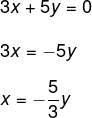
Substituindo na equação II, temos que:
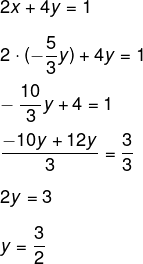
Conhecendo o valor de y, encontraremos o valor de x:
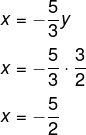
Agora calcularemos x + y:
![]()
Questão 2
Uma matriz só possui inversa quando o seu determinante é diferente de 0. Analisando a matriz abaixo, quais são valores de x que fazem com que a matriz não admita inversa?
![]()
a) 0 e 1.
b) 1 e 2.
c) 2 e – 1.
d) 3 e 0.
e) – 3 e – 2.
Resolução:
Alternativa b.
Calculando o determinante de A, queremos os valores em que det(A) = 0.
det(A) = x ·(x – 3) – 1 · ( – 2)
det(A) = x² – 3x + 2
det(A) = x² – 3x + 2 = 0
Resolvendo a equação do 2º grau, temos que:
- a = 1
- b = – 3
- c = 2
Δ = b² – 4ac
Δ = (– 3) ² – 4·1·2
Δ= 9 – 8
Δ = 1