Determinantes

O determinante de uma matriz possui várias aplicações atualmente. Utilizamos o determinante para verificar se três pontos estão alinhados no plano cartesiano, para calcular áreas de triângulos, para resolução de sistemas lineares, entre outras aplicações na matemática. O estudo de determinantes não se limita à matemática, há algumas aplicações na física, como no estudo de campos elétricos.

Calculamos determinantes somente de matrizes quadradas, ou seja, matrizes em que a quantidade de colunas e a quantidade de linhas são iguais. Para calcular o determinante de uma matriz, precisamos analisar a ordem dela, ou seja, se ela é 1x1, 2x2, 3x3 e assim sucessivamente, quanto maior a sua ordem, mais difícil será encontrar o determinante. No entanto, há métodos importantes realizar-se o exercício, como a regra de Sarrus, utilizada para calcular-se determinantes de matrizes 3x3.

Leia também: Processo para resolução de um sistema linear m x n

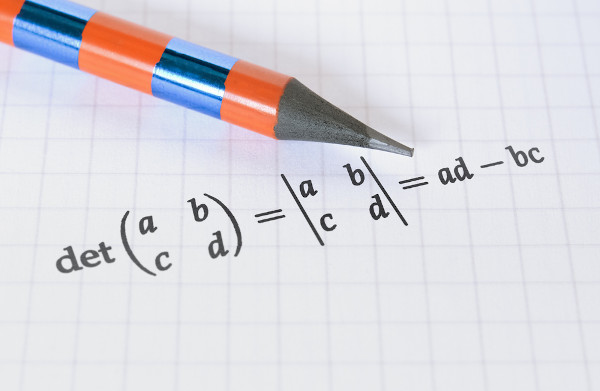
Tópicos deste artigo

• 1 - Determinante de matriz de ordem 1
• 2 - Determinantes de matrizes de ordem 2
• 3 - Determinante de matriz de ordem 3
  • Regra de Sarrus
• 4 - Propriedades do determinante
  • 1ª propriedade
  • 2ª propriedade
  • 3ª propriedade
  • 4ª propriedade
• 5 - Exercícios resolvidos

Determinante de matriz de ordem 1

Uma matriz é conhecida como de ordem 1 quando possui exatamente uma linha e uma coluna. Quando isso ocorre, a matriz possui um único elemento, o a₁₁. Nesse caso o determinante da matriz coincide com esse seu único termo.

A = (a₁₁)

det(A) = | a₁₁ | = a₁₁

Exemplo:

A = [2]

det(A) = |2| = 2

Para calcular-se determinantes de matrizes de ordem 1, é necessário então apenas conhecer o seu único elemento.

Determinantes de matrizes de ordem 2

A matriz quadrada 2x2, conhecida também como matriz de ordem 2, possui quatro elementos, nesse caso, para calcular o determinante, é necessário conhecermos o que é a diagonal principal e a diagonal secundária.

Para calcular o determinante de uma matriz de ordem 2, calculamos a diferença entre o produto dos termos da diagonal principal e os termos da diagonal secundária. Utilizando o exemplo algébrico que construímos, o det(A) será:

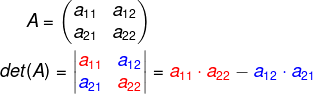
Exemplo:

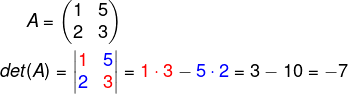
Determinante de matriz de ordem 3

A matriz de ordem três é mais trabalhosa para obter-se o determinante do que as anteriores, na verdade, quanto maior a ordem de uma matriz, mais difícil será esse trabalho. Nela é necessário utilizar o que conhecemos como regra de Sarrus.

• Regra de Sarrus

A regra de Sarrus é um método para calcular-se determinantes de matrizes de ordem 3. É necessário seguir alguns passos, sendo o primeiro duplicar as duas primeiras colunas no final da matriz, conforme o exemplo a seguir.

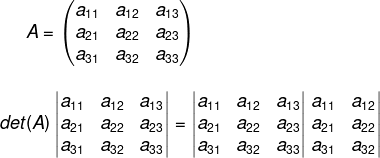
Agora vamos multiplicar os termos de cada uma das três diagonais que estão no mesmo sentido da diagonal principal.

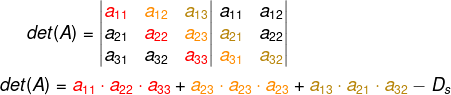
Realizaremos um processo parecido com a diagonal secundária e as outras duas diagonais que estão no mesmo sentido que ela.

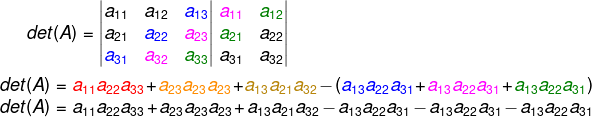
Note que os termos da diagonal secundária estão sempre acompanhados com o sinal negativo, ou seja, sempre trocaremos o sinal do resultado da multiplicação dos termos da diagonal secundária.

Exemplo:

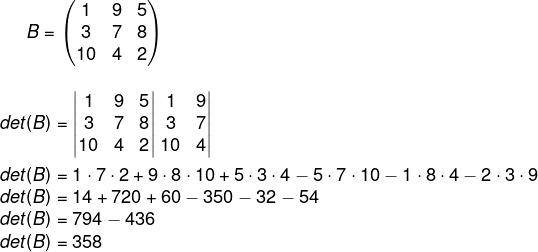
Veja também: Teorema de Binet – processo prático para a multiplicação de matrizes

Propriedades do determinante

• 1ª propriedade

Caso uma das linhas da matriz seja igual a 0, então o seu determinante será igual a 0.

Exemplo:

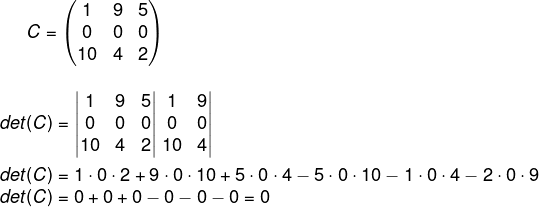
• 2ª propriedade

Seja A e B duas matrizes, det(A·B) = det(A) · det(B).

Exemplo:

Calculando os determinantes separados, temos que:

det(A) = 2 · (-6) – 5 · 3
det(A) = -12 – 15 = -27

det(B) = 4 · 1 – 2 · (-2)
det(B) = 4 + 4 = +8

Então det(A) · det(B) = -27 · 8 =  -216

Agora vamos calcular det(A·B)

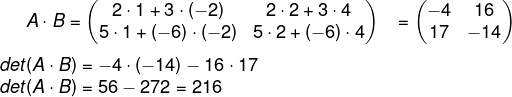
• 3ª propriedade

Seja A uma matriz e A’ uma nova matriz construída trocando-se as linhas da matriz A, então det(A’) =  -det(A), ou seja, ao inverter-se a posição das linhas de uma matriz, o seu determinante terá o mesmo valor, porém de sinal trocado.

Exemplo:

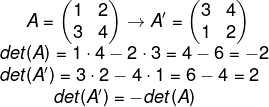
• 4ª propriedade

Linhas iguais ou proporcionais fazem com que o determinante da matriz seja igual a 0.

Exemplo:

Note que, na matriz A, os termos da linha dois são o dobro dos termos da linha um.

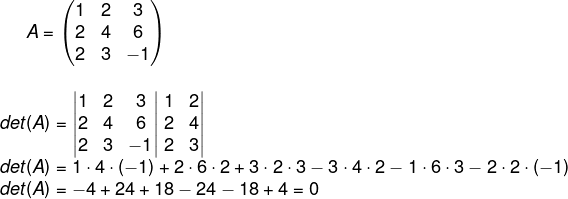
Acesse também: Aplicação das matrizes nos vestibulares

Exercícios resolvidos

Questão 1 - (Vunesp) Considerando as matrizes A e B, determine o valor de det(A·B):

a) -1

b) 6

c) 10

d) 12

e) 14

Resolução

Alternativa E

Sabemos que det(A·B) = det(A) · det(B):

det(A) = 1· 4 – 2 · 3 = 4 – 6 = -2
det(B) = -1 · 1 – 3 · 2 = -1 – 6 = -7

Então temos que:
det(A·B) = det(A) · det(B)
det(A·B) = -2 (-7) = 14

Questão 2 - Dada a matriz A, qual deve ser o valor de x para que det(A) seja igual a 0?

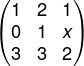
a) 1/2

b) 1/3

c) 1/9

d) 3
e) 9

Resolução

Alternativa B

Calculando o determinante de A, temos que:

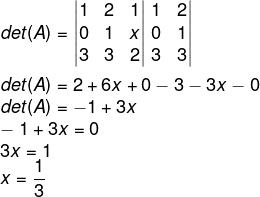
Por Raul Rodrigues de Oliveira
Professor de Matemática